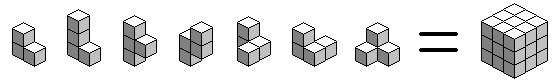Existen diseños que han hecho uso de este
puzzle tridimensional. Por ejemplo, en la siguiente imagen podemos apreciar el
diseño de una mesa de salón del divulgador de las matemáticas norteamericano
Michael Serra basado en las piezas del “cubo soma”. Cinco de las piezas (todas,
salvo las piezas L y Z) conforman la parte de apoyo de la mesa, sobre la que se
sitúa la parte plana, en este caso el cristal, y las otras dos piezas del
puzzle quedan de acompañamiento, ya sea como sencillos asientos, como mesitas
auxiliares o simplemente como complementos decorativos.
Diseño de una mesa utilizando las piezas del “cubo soma”, por Michael Serra
Maqueta de la colocación de las piezas del “cubo soma” en el diseño anterior, realizado con pequeñas piezas de madera del juego
El proyecto “Polyomino” presentado en el Festival del Diseño
de Londres (London Design Festival) el pasado mes de septiembre (2014), como
fruto de una colaboración entre el diseñador de complementos inglés Ally
Capellino y el arquitecto inglés Seng Watson, también ha encontrado la
inspiración y la forma en este puzzle geométrico cuyas siete piezas están
formadas por la unión de cubos.
Ally Capellino le encargó a Seng Watson la realización de
una serie de “stands” para colocar, durante el London Design Festival, sus
bolsos y otros complementos en las tiendas que Capellino tiene en Londres. Una
de las inspiraciones del proyecto “Polyomino” fue la arquitectura “brutalista”
londinense de los años 1960, en la que está también inspirada la colección
otoño/invierno 2014 de Capellino. El arquitecto decidió realizar los “stands”
con las piezas del “cubo soma”, a partir de cubos de 27.250 mm3 de “papercrete”
(hormigón de papel), una mezcla de cemento y papel, que hace que las piezas del
diseño tengan el aspecto crudo del hormigón, pero sean a la vez ligeras y
manejables.
Las siete piezas del proyecto “Polyomino” realizadas en hormigón de papel
“Stands” del proyecto “Polyomino” con bolsos y complementos en una de las tiendas de Ally Capellino en Londres
Curiosamente, el nombre del proyecto, “Polyomino”, es
confuso, puesto que las piezas del “cubo soma” no son poliominós (es decir,
figuras geométricas planas formadas conectando dos o más cuadrados por alguno
de sus lados), sino que son policubos (esto es, figuras geométricas tridimensionales
que se forman al unir dos o más cubos por alguna de sus caras). Solo cuatro de
las piezas del “cubo soma” podrían ser consideradas poliominós, puesto que son
las cuatro piezas “planas” del puzzle, aquellas que pueden colocarse para que
tengan solo la altura de un cubo, y no más altura, como ocurre en las otras
tres piezas (véanse las piezas del “cubo soma” de la siguiente imagen).
Pero dejemos de lado, los diseños basados en el “cubo soma”,
y centrémonos en el propio puzzle geométrico tridimensional. Como ya
comentábamos en la entrada “Un delicioso puzzle de chocolate” del Cuaderno de
Cultura Científica, el “cubo soma” es un juego de ingenio relativamente
moderno, que fue inventado en 1933 por el poeta, matemático, diseñador e
inventor danés Piet Hein (1905-1996).
Fue durante una conferencia sobre mecánica cuántica del
premio Nobel de Física, Werner Heisenberg (1901-1976), cuando Piet Hein se dio
cuenta de que con todos los policubos irregulares formados por 4, o menos,
cubos (matemáticamente que sean irregulares quiere decir que cada uno de esos
policubos es no convexo, es decir, que dados dos puntos cualesquiera del mismo
no es cierto que todos los puntos que están en el segmento que los une estén
también en el policubo, por tanto hay que descartar los regulares, que son o
una serie de cubos alineados, uno, dos o tres, o un “cuadrado” formado por
cuatro cubos), que son siete, se podía formar un cubo 3x3x3.
Las piezas del “cubo soma”
Las siete piezas del juego de ingenio que Piet Hein bautizó
con el nombre de “cubo soma” son un policubo formado por tres cubos (con la
forma de una L “corta”) y seis policubos formados por cuatro cubos (una esquina
o trípode, una L “larga”, una T, una Z y otras dos piezas que son una la imagen
especular de la otra).
Este puzzle geométrico, que consiste en formar un cubo de
tamaño 3x3x3 con los siete policubos irregulares, admite 240 soluciones
distintas. Y fueron los matemáticos ingleses John H. Conway y Richard K. Guy
quienes obtuvieron la lista completa de las 240 soluciones, “en una tarde lluviosa
de 1961”.
A continuación, mostraremos el estudio que realizaron los
dos matemáticos, y que aparece en el libro Winning ways for your mathematical
plays de Elwyn R. Berlekamp, John H. Conway y Richard K. Guy, sobre las
posibles posiciones de cada una de las siete piezas del “cubo soma” dentro del
cubo final de tamaño 3x3x3 y que les permitió conocer que hay 240 soluciones
posibles, y obtenerlas explícitamente.
Para empezar, como vemos en la siguiente imagen, asocian
cada pieza del puzzle a un número y un color, para poder identificarlas.
La pieza L “corta” es blanca y su número es el 1, la L es amarilla y el 2, la pieza T es verde y tiene el 3, la Z debería de ser naranja, aunque nosotros a falta de cubos naranjas la hemos fabricado multicolor, y su número es el 4, la pieza azul tiene el 5 y su imagen especular es roja con el número 6, y finalmente, la pieza esquina es negra y su número es el 7
Si observamos el cubo de tamaño 3x3x3 que es el objeto final
de este rompecabezas, este tiene 8 cubos vértice (que aparecen en rojo en la
siguiente imagen), 12 cubos laterales (en verde), 6 cubos cara (en blanco) y un
cubo central (que no se ve, ya que está en el interior).
Pero dejemos ya esta parte matemática del puzzle de Piet
Hein, relacionada con la combinatoria (el cálculo del número de soluciones del
juego), y terminemos la entrada con un par de ejemplos de la presencia del
“cubo soma” en el arte.
La primera obra de arte (que aparece en la siguiente imagen)
es la obra “Letter From the New World to theOld World” de la artista danesa
Simon Dybbroe Møller.
“Letter From the New World to the Old World”, Simon Dybbroe Møller
El artista estadounidense Arnold Martin ha utilizado el
puzzle geométrico en su obra “Anatomy of a Cube or This is Not a Stack of
Crates”, de su instalación IN-KOM-PRI-HEN-SUH-BUHL.
“Anatomy of a Cube or This is Not a Stack of Crates”, Arnold Martin